Kali ini akan diulas tentang rumus tabung, mulai dari rumus volume tabung hingga rumus luas permukaan dan selimut tabung. Lengkap beserta bagaimana cara menghitung dan contoh soalnya agar kita lebih paham dan mengerti.
Tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki 3 sisi dan 2 rusuk. Kedua lingkaran disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung. Radius, Diameter, dan Tinggi Sebuah Silinder serta Dimensi sebuah silinder atau tabung dinyatakan dengan besaran radius atau diameter penampang tabung dan tinggi tabung.
Ciri-ciri Tabung
- Mempunyai dua buah rusuk.
- Mempunyai alas dan tutup yang berbentuk lingkaran yang sama besar.
- Memiliki tiga buah sisi yaitu dua buah sisi berbentuk lingkaran dan satu sisi selimut berbentuk persegi panjang.
Rumus Tabung
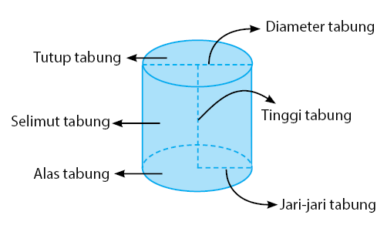
Dan untuk menghitung ukuran tabung baik volume, luas permukaan hingga luas selimut tabung, dibutuhkan sebuah rumus agar penghitungan bisa lebih mudah dan cepat. Langsung saja simak rumus rumus tabung berikut ini, lengkap beserta contoh soalnya.
Rumus Volume Tabung
Untuk mengetahui volume ataupun isi dari sebuah tabung maka kita harus mengetahui jari-jari ataupun diameter dari penampang (alas/tutup) tabung tersebut. Perlu diingat bahwa diameter nilainya sama dengan dua kali jari-jari (diameter = 2 x jari-jari).
Volume tabung dapat diketahui dengan cara mengalikan luas alas abung dengan tinggi dari tabung tersebut. Dikarenakan alas tabung memiliki bentuk lingkaran, maka rumus volumenya dapat disusun dengan mengalikan rumus luas lingkaran dengan tinggi tabung. Berikut rumusnya,
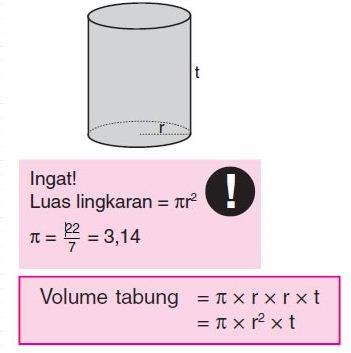
V = phi x jari-jari x jari-jari x tinggi
V = π x r x r x t
V = πr2 x t
Jika yang diketahui adalah diameternya, maka rumusnya bisa diubah menjadi berikut,
V = 1/4 x π x diameter x diameter x t
Keterangan :
Π = phi (22/7 atau 3,14)
r = jari-jari alas
t = tinggi tabung
Perlu diperhatikan bahwa dalam menghitung volume tabung menggunakan rumus di atas, dimensi radius (atau diameter) dan tingginya harus dalam satuan yang sama. Satuan volume adalah satuan panjang kubik misalnya millimeter kubik (mm3), centimeter kubik (cm3) , meter kubik (m3), dan lain sebagainya.
Rumus Luas Permukaan Tabung
Luas permukaan tabung atau silinder merupakan luas dari jumlah sisi-sisi yang di miliki tabung yaitu dua buah alas lingkaran yang sama besar dan satu buah selimut berbentuk persegi panjang.

Rumus luas permukaan tabung = 2 x π x r x ( t + r )
Rumus Luas Selimut Tabung
2 x π x r x t
Keterangan :
π = phi ( 22/7 atau 3,14 ).
r = jari-jari alas.
t = tinggi tabung.
- Rumus luas selimut diatas diperoleh dari = Keliling lingkaran x tinggi tabung.
- Rumus luas permukaan tabung di peroleh dari = dua kali luas lingkaran + luas selimut yang berbentuk persegi panjang.
Contoh Soal
Setelah kita mengetahui rumus volume tabung dan rumus luas permukaan tabung, kini saatnya menguji seberapa jauh kita dalam memahami rumus tabung diatas. Berikut ini contoh soal dan jawabannya sebagai media untuk memudahkan kita dalam memahami cara menghitung volume tabung dan luasnya,
#Contoh Soal 1
diketahui sebuah tabung memiliki jari-jari 7 cm dan memiliki tinggi 5 cm. hitunglah luas permukaan dan volume dari tabung tersebut.
Penyelesaian:
luas permukaan tabung = π x r2
luas permukaan tabung = 22/7 x 72
luas permukaan tabung = 154 cm2
untuk mengetahui volume tabung kita cukup mengalikan luas permukaan alas dengan tinginya:
V = Luas permukaan x t
V = 154 x 5 = 770 cm3
#Contoh Soal 2
Bila jari-jari dari sebuah tabung diketahui 21 cm dan tingginya aalah 13, maka hitunglah volume dari tabung tersebut!
Penyelesaian:
V = πr2 x t
V = 22/7 x 212 x 13
V = 1386 x 13
V = 18018 cm3
#Contoh Soal 3
Diketahui sebuah tabung memiliki jari-jari 7 cm dan memiliki tinggi 5 cm. hitunglah luas permukaan dan volume dari tabung tersebut ?
Penyelesaian:
luas permukaan tabung = π x r2
luas permukaan tabung = 22/7 x 72
luas permukaan tabung = 154 cm2
untuk mengetahui volume tabung kita cukup mengalikan luas permukaan alas dengan tinginya:
V = Luas permukaan x t
V = 154 x 5 = 770 cm3
#Contoh Soal 4
Diketahui jari-jari alas suatu tabung adalah 12 cm. Jika tinggi tabung tersebut 10 cm, tentukan volume tabung tersebut.
Diketahui :
r = 12 cm
t = 10 cm.
Ditanyakan : volume tabung?
Penyelesaian:
Volume tabung = pr2t
= 3,14 ? (12)2 ? 10
= 4.521,6 cm3
Jadi, volume tabung tersebut adalah 4.521,6 cm3.
#Contoh Soal 5
Sebuah tabung memiliki jari-jari 7 cm. Jika tingginya 12 cm, hitunglah volume tabung tersebut!
V = πr² x t = 22/7 x 7² x 12 = 22 x 7 x 12 = 1.848 cm³
#Contoh Soal 6
Berapa volume sebuah tabung yang memiliki diameter 20 cm dan tinggi 28 cm? (Petunjuk : volume silinder = phi x radius x radius x tinggi).
Jawab :
Radius silinder adalah setengah dari diameter yaitu 10 cm.
Volume tabung = (22/7) x 10 cm x 10 cm x 28 cm = 8.800 cm³.
#Contoh Soal 7
Apabila jari-jari dari sebuah tabung diketahui 21 cm dan tingginya aalah 13 cm, maka hitunglah volume dari tabung tersebut.
Penyelesaian:
V = πr2 x t
V = 22/7 x 212 x 13
V = 1386 x 13
V = 18018 cm3
#Contoh Soal 8
Putri memiliki tangki minyak berbentuk tabung dengan tinggi 2 meter. Jika tangki tersebut diisi minyak sampai penuh, tangki tersebut dapat menampung 2260,8 liter minyak. Berapa volume tangki minyak milik Putri ?
Penyelesaian:
Diketahui : Volume (v) = 2260,8 liter =2.260.800 cm3
Tinggi (t ) = 2 m = 200 cm
Ditanya : jari-jari (r)
Jawab :
Jadi jari-jari tangki tersebut adalah 60cm.
#Contoh Soal 9
Sepotong kayu dibentuk menjadi sebuah silinder dengan luas penampang 240 cm2. Silinder kayu tersebut tingginya 50 cm. Berapa volume silinder kayu tersebut? (Petunjuk: volume silinder = luas penampang lingkaran x tinggi).
Jawab :
Volume silinder kayu = 240 cm2 x 50 cm = 12.000 cm³.
#Contoh Soal 10
Diketahui luas alas suatu tabung adalah 616 cm². Berapa volume tabung tersebut jika tingginya 8 cm?
Volume = luas alas x tinggi = 616 x 8 = 4.928 cm³.
#Contoh Soal 11
Sebatang besi sepanjang 7 meter mempunyai penampang berbentuk lingkaran dengan diameter 1 cm. Berapa volume batang besi tersebut dalam centimeter kubik? (Petunjuk: volume silinder = pi x radius x radius x tinggi).
Jawab :
Panjang besi = tinggi silinder yaitu 7 m = 700 cm.
Radius silinder = setengah kali diameter batang besi yaitu 0,5 cm.
Volume batang besi = (22/7) x 0,5 cm x 0,5 cm x 700 cm = 550 cm³.
#Contoh Soal 12
Sekeping koin logam memiliki tebal 1,4 mm dan diameter 20 mm. Berapa volume koin tersebut? (Petunjuk: volume silinder = pi x radius x radius x tinggi).
Jawab :
Tebal koin = tinggi silinder yaitu 1,4 mm.
Radius koin = setengah kali diameter yaitu 10 mm.
Volume koin = (22/7) x 10 mm x 10 mm x 1,4 mm = 440 mm³.
#Contoh Soal 13
Sebongkah es batu dicetak membentuk silinder dengan ukuran jari-jari silinder dan tebalnya sama yaitu 35 cm. Berapa volume silinder es tersebut? (Petunjuk: volume silinder = pi x radius x radius x tinggi).
Jawab :
Radius = jari-jari silinder yaitu 35 cm.
Tinggi silinder = tebal silinder = 35 cm.
Volume silinder es = (22/7) x 35 cm x 35 cm x 35 cm = 134.750 cm³.
#Contoh Soal 14
Sebuah baja dengan panjang 8 meter memiliki penampang yang berbentuk lingkaran dengan diameternya 6 cm. Hitunglah volume batang baja tersebut dalam satuan centimeter.
Jawab :
Volume Silinder = π x r² x t
Panjang baja = tinggi silinder yakni 8 meter = 800 cm.
r atau radius = setengah diameter = 6 : 2 = 3 cm.
Volume batang baja = (22/7) x 3 x 3 x 800 = 22.628,57 cm³.
#Contoh Soal 15
Shena mengisi botol berbentuk tabung dengan susu sebanyak 6,30 liter ternyata setelah botol penuh susu tersisa 0,02 liter. Jika jari-jari botol 1 dm, berapa tinggi botolnya?
Jawab:
Kita perlu tahu isi botol saat terisi susu penuh yakni= 6,30- 0,04= 6,28 liter= 6,28 dm3
Maka V= πr2 x t
6,28=3,14 x 12x t
t=6,28/3,14=2 dm
Jadi tinggi botol tersebut adalah 2dm.
#Contoh Soal 16
Sebatang pipa PVC berbentuk tabung memiliki panjang yakni 14 meter dan mempunyai jari-jari 3 cm. Berapa liter volume pipa PVC tersebut?
Penyelesaian:
Diketahui : jari-jari (r) = 3 cm
Tinggi (t ) = 14 m = 1400 cm
Ditanya : Volume tabung (v)
Jawab :
Jadi volume pipa tersebut adalah 39,6 liter
Jadi volume tabung adalah 18018 cm.
#Contoh Soal 17
Terdapat sebuah tabung dengan jari-jari berukuran 7 cm dan tingginya 18 cm, berapakah volume tabung tersebut?
jawaban:
Sesuai rumus V = ∏ x r² x t maka dengan mudah kita bisa menyelsaikan soal tersebut.
Dari soal tersebut diketahui bahwa:
jari-jari (r)= 7 cm
tinggi (t)= 18 cm
maka
V=π x r² x t
= 22/7 x 7² x 18
= 2771 cm³
#Contoh Soal 18
Berapakah volume sebuah tabung yang mempunyai diameter 40 cm dan tinggi 56 cm?
Jawab :
diameter = 40 cm, karena r = 1/2 diameter maka r = 20 cm
tinggi = 56 cm
Volume Tabung = π x r² x t
= (22/7) x 20cm² x 56 cm
= (22/7) x 20 x 20 x 56
= (22/7) x 22.400
= 70.400 cm³.
Demikianlah rumus rumus tabung secara lengkap beserta contoh soalnya, mulai dari rumus volume tabung, rumus luas tabung hingga selimut tabung. Semoga artikel ini bermanfaat dan bisa menambah wawasan pengetahuan kita mengenai rumus bagaimana cara menghitung volume dan luas sebuah tabung dengan benar.
Facebook Tweet Whatsapp