Kali ini akan dibahas mengenai rumus trapesium, baik rumus luas trapesium maupun rumus keliling trapesium, lengkap besert contoh soal dan bagaimana cara menghitungnya yang benar menggunakan masing masing rumus yang tersedia. Diulas juga pengertian, sifat dan jenis jenis trapesium agar lebih paham dan mengerti secara keseluruhan.
Trapesium adalah bangun datar segi empat yang dibentuk dengan empat dua buah rusuk / sisi yang dua diantaranya saling sejajar tetapi tidak sama panjang. Trapesium hanya memiliki 1 simetri putar. Ada beberapa sifat sifat khusus yang dimiliki trapesium, berikut ini diantaranya,
Sifat Sifat Trapesium :
- Termasuk bangun datar dua dimensi.
- Merupakan bangun datar yang berbentuk segi empat.
- Mempunyai rusuk yang jumlahnya empat dan dua yang lainnya saling sejajar.
- Mempunyai satu simetri putar.
- Tidak mempunyai simetri lipat, namun terkecuali trapesium sama kaki.
- Memilik tiga jenis trapesium yaitu trapesium siku siku, trapesium sembarang dan trapesium sama kaki.
- Memiliki 4 sisi dan 4 titik sudut.
- Memiliki sepasang sisi yang sejajar tapi tidak ama panjang.
- Memiliki sudut di antara sisi sejajarnya sebesar 180°.
Jenis Jenis Trapesium :
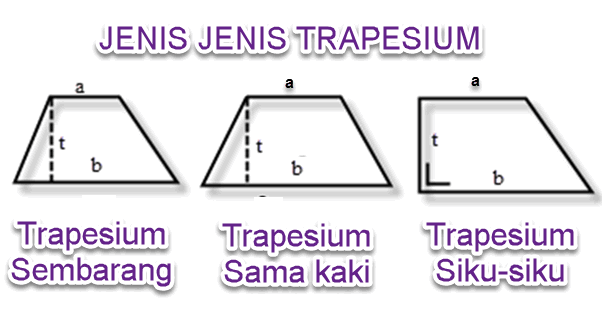
Ada tiga jenis trapesium, yaitu trapesium sembarang, trapesium sama kaki dan trapesium siku-siku. Berikut penjelasannya,
- Trapesium sembarang, trapesium yang keempat rusuknya tidak sama panjang serta tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
- Trapesium sama kaki, trapesium yang memiliki sepasang rusuk yang sama panjang, di samping memiliki sepasang rusuk yang sejajar. Trapesium ini memiliki 1 simetri lipat dan 1 simetri putar.
- Trapesium siku-siku, trapesium yangdua di antara keempat sudutnya adalah sudut siku-siku. Rusuk-rusuk yang sejajar tegak lurus dengan tinggi trapesium ini serta tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
Rumus Trapesium
Trapesium merupakan bangun datar yang pengerjaannya dapat menggunakan rumus pythagoras. Rumus pythagoras tersebut dikombinasikan dengan rumus trapesium. Namun penggunaan rumus pythagoras berguna ketika salah satu sisi trapesium belum diketahui.
Langsung saja berikut ini rumus luas trapesium dan rumus keliling trapesium beserta penjelasan, contoh soal dan bagaimana cara menghitungnya secara lengkap,
Rumus Luas Trapesium
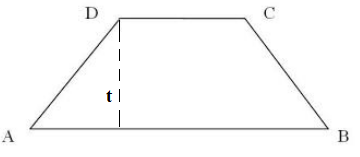
Rumus Luas Trapesium :
1/2 x jumlah sisi sejajar x tinggi
Keterangan :
Jumlah sisi sejajar = AB + CD ( lihat gambar di atas )
Tinggi = t
Rumus Keliling Trapesium

Rumus Keliling Trapesium :
AB + BC + CD +DA
Keterangan :
Keliling trapesium merupakan jumlah seluruh sisi-sisinya, AB, BC, CD, DA adalah sisi-sisi trapesium ( Lihat gambar )
Contoh Soal Trapesium
Setelah kita mengetahui mengeni rumus luas trapesium dan rumus keliling trapesium, kini saatnya menguji pemahaman kita dengan mengerjakan contoh soal. Berikut ini kumpulan contoh soal trapesium dan jawabannya agar kita lebih paham bagaimana cara menghitung trapesium menggunakan rumus yang benar, baik ukuran luas dan lingkarannya,
Perlu diketahui bahwa dalam penyelesaian menghitung luas trapesium terkadang memerlukan juga rumus-rumus bangun datar yang lain seperti rumus luas dan keliling persegi panjang dan bujursangkar, rumus luas dan keliling segitiga, dan juga rumus phytagoras.
#Contoh Soal 1
Perhatikan gambar dibawah ini!
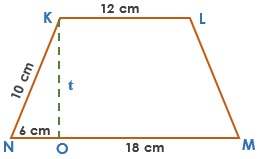
Hitunglah luas dan keliling trapesium sama kaki diatas!
Jawab:
Karena trapesium KLMN diatas merupakan trapesium sama kaki maka panjang LM = KN = 10 cm.
Sehingga kelilingnya:
Keliling = KL + LM +MN + KN
Keliling = 12 + 10 + (18 + 6) + 10 = 56 cm
Luas trapesium:
Untuk menghitung luasnya, terlebih dahulu kita harus mengetahui tinggi trapesium tersebut (panjang sudut K dan O). Perhatikan pada gambar, sudut N K O membentuk sebuah segitiga siku-siku sehingga untuk mencari panjang sudut K dan O digunakan rumus Phytagoras berikut:
K O = tinggi trapesium = 8 cm.
Sehingga:
Luas = ½ × jumlah sisi sejajar × tinggi
Luas = ½ × (KL + MN) × KO
Luas = ½ × (12 + 24) × 8 = 144 cm².
#Contoh Soal 2
Sebuah trapesium diketahui mempunyai panjang sisi-sisi sejajar masing-masing adalah 8 cm dan 20 cm dan ukuran tingginya 12 cm. Hitunglah berapa luas bangun trapesium ini ?
Penyelesaian:
Luas = ½ x ( Jumlah sisi sejajar ) x t
Luas = ½ x (8 cm + 20 cm) x 12 cm
Luas = ½ x 28 x 12
Luas = ½ x 336 cm
Luas = 168 cm2
Jadi luas bangun trapesium di atas adalah 168 cm2
#Contoh Soal 3
Perhatikan gambar berikut ini !
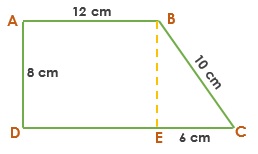
Rumus Luas dan Keliling Trapesium Lengkap dengan Contoh Soal
Keliling dan luas pada trapesium diatas adalah …
Jawab:
Keliling trapesium:
Perhatikan gambar diatas, ABED membentuk bangun persegi panjang, maka panjang AB = DE = 12 cm,
sehingga CD = CE + DE = 12 + 6 = 18 cm
Keliling = AB + BC + CD + DA
Keliling = 12 + 10 + 18 + 8 = 48 cm
Luas trapesium:
L = ½ × jumlah rusuk sejajar × tinggi
(BE adalah tinggi trapesium, karena ABED membentuk bangun persegi panjang, maka panjang AD = BE = 8 cm)
Sehingga,
L = ½ × (AB + CD) × BE
L = ½ × (12 + 18) × 8 = 120 cm²
#Contoh Soal 4
Jika diketahui sebuah trapesium dengan tinggi 15 cm. dan panjang sisi sejajarnya adalah 16 cm dan 24 cm. berapakah luas trapesium tersebut ?
Diketahui:
t = 15 cm
a = 16 cm
b = 24 cm.
Ditanya: L..?
Jawab:
L = ½ (a + b) × t
L = ½ (16 + 24) × 15
L = ½.40 × 15
L= 20 × 15 = 300 cm2
Jadi luas dari bangun trapesium di atas adalah 300 cm2.
#Contoh Soal 5
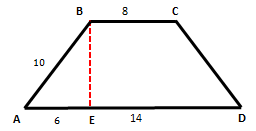
Hitung keliling dan luas trapesium sama kaki pada gambar dibawah ini
Jawab
Karena trapesium tersebut adalah trapesium sama kaki, maka panjang CD = panjang AB = 10 satuan.
Panjang Keliling trapesium = AB + BC + CD + DA = 10 + 8 + 10 + (6+14) = 48 satuan
Untuk mendapatkan tinggi BE digunakan rumus phytagoras :
AB2 = AE2 + BE2
102 = 62 + BE2
100 = 36 + BE2
BE2 = 64
BE = 8 satuan
Luas Trapesium = jumlah sisi sejajar x tinggi / 2
Luas trapesium = (BC + AD) x BE / 2
= (8 + 20) x 8 / 2 = 112 satuan luas.
#Contoh Soal 6
Perhatikan pernyataan trapesium dan layang-layang berikut ini.
- Trapesium dengan tinggi 12 cm dan panjang sisi sejajarnya 18 cm dan 24 cm.
- Layang-layang dengan dengan panjang diagonalnya adalah (10 + 10) cm dan (16 + 8) cm.
Diantara kedua bangun di atas, bangun manakah yang lebih luas ?
Diketahui trapesium:
a = 18 cm
b = 24 cm
t = 12 cm.
Ditanya: L…?
Jawab:
L = ½ (a + b) × t
L = ½ (18 + 24) × 12
L = ½.42 × 12
L = 21 × 12
L = 252 cm2
Jadi luas trapesium adalah 252 cm2.
Diketahui layang-layang:
d1 = (10 + 10) cm
d2 = (16 + 8) cm
Ditanya: L..?
Jawab:
L = ½ × d1 × d2
L = ½ × (10 + 10) × (16 + 8)
L = ½ × 20 × 24
L = ½ × 480
L = 240
Jadi luas layang-layang di atas adalah 240 cm2.
Kesimpulannya yaitu lebih luas bangun trapesium, dengan luas 252 cm2.
#Contoh Soal 7
Sebuah trapesium memiliki sisi sejajar 6 cm dan 14 cm serta tinggi 4 cm. Berapakah luas trapesium tersebut?
Jawab
Luas trapesium = jumlah sisi sejajar x tinggi / 2 = (6+14) x 4 / 2 = 40 cm2.
#Contoh Soal 8
Jika panjang kedua sisi miring pada trapesium pada soal 1 adalah 5 cm, berapakah keliling trapesium?
Jawab
Keliling trapesium = panjang semua rusuk = 6 + 14 + 5 + 5 = 30cm.
#Contoh Soal 9
Diketahui bangun layang-layang dengan panjang diagonal yaitu 30 cm dan 26 cm serta bangun trapesium dengan panjang sisi sejajar yaitu 30 cm dan 40 cm. Jika luas kedua bangun tersebut sama, berapakah tinggi bangun trapesium tersebut?
Diketahui:
d1 = 30 cm,
d2 = 26 cm,
a = 30 cm
b = 40 cm.
Jawab:
L layang-layang= ½ × d1 × d2
L = ½ × 30 × 26
L = ½ × 780
L= 390.
Jadi luas bangun trapesium adalah 390 cm2.
t trapesium= 2L : (a + b)
t = 2.390 : (30 + 40)
t = 780 : 70
t = 11,1
Jadi tinggi trapesium yaitu 11,1 cm.
#Contoh Soal 10
Pada hari minggu pagi warga di desa pak Bambang melakukan suatu kerja bakti. Warga mengecat atap gapura yang berbentuk trapesium pada sisi depan dan belakang. Atap gapura tersebut memiliki panjang sisi sejajarnya yaitu 4 m dan 3 m dan jarak kedua sisi tersebut 0,9 m. berapakah luas atap gapura yang dicat oleh warga ?
Diketahui:
a = 4 m
b = 3 m
t = 0,9 m.
Ditanya: L..?
Jawab:
L = ½ (a + b) × t
L = ½ (4 + 3) × 0,9
L = ½.7 × 0,9
L = 3,5 × 0,9
L = 3,15 m.
#Contoh Soal 11
Pak Ade mempunyai tanah kosong yang berbentuk trapesium. Panjang sisi tanah yang sejajar adalah 10 meter dan 16 meter dan luasnya 156 m2. Berapakah lebar tanah pak Ade tersebut?
Diketahui:
a = 10 m
b = 16 m
L = 156 m2
Ditanya: Lebar tabah?
Jawab:
t = 2L : (a + b)
t = 2.156 : (10 + 16)
t = 312 : 26
t = 12
Jadi lebar tanah pak Ade adalah 12 meter.
#Contoh Soal 12
Salah satu sisi atap rumah pak Budi berbentuk trapesium. Panjang sisi bawah adalah 8 meter dan panjang sisi atas adalah 5 meter. Jika tinggi trapesium tersebut 4 meter, berapakah luasnya?
Diketahui:
a = 8 m
b = 5 m
t = 4 m.
Ditanya: L..?
Jawab:
L = ½ (a + b) × t
L = ½ (8 + 5) × 4
L = ½.13 × 4
L = 6,5 × 4
L = 26 m2
Jadi luas atap rumah pak Budi adalah 26 m2.
#Contoh Soal 13
Diketahui luas trapesium 104 cm2. Panjang sisi sejajar 15 cm dan 11 cm. berapakah tinggi trapesium tersebut ?
Diketahui:
a = 15 cm
b = 11 cm,
L = 104 cm2
Ditanya: t…?
Jawab:
t = 2L : (a + b)
t = 2.104 : (15 + 11)
t = 208 : 26
t = 8
Jadi tinggi trapesium di atas adalah 8 cm.
#Contoh Soal 14
Sebuah trapesium mempunyai panjang sisi-sisi sejajar berturut-turut 4 cm dan 10 cm serta tinggi 5 cm, maka berapakah luas trapesium tersebut?
Penyelesaian:
Luas = ½ x (a1 + a2) x t
Luas = ½ x (4 cm + 10 cm) x 5 cm
Luas = ½ x 14 x 5
Luas = 35 cm
#Contoh Soal 15
Sebuah bangun datar trapesium sama kaki dengan panjang sisi sejajar 4 cm dan 10 cm, kemudian sisi miringnya 5 cm, hitunglah kelilingnya ?
Diketahui :
sisa a = 5 cm
sisi b = 4 cm
sisi c = 5 cm
sisi d = 10 cm
Jawab :
K = sisi a + sisi b + sisi c + sisi d
K = 5 cm + 4 cm + 5 cm + 10 cm
K = 24 cm
#Contoh Soal 16
Sebuah trapesium mempunyai panjang sisi-sisi sejajar berturut-turut 4 cm dan 10 cm serta tinggi 5 cm. maka, berapakah luas trapesium tersebut?
Diketahui:
sisi sejajar: a1 = 4 cm, a2 = 10 cm
t= 5 cm
Ditanya: L…?
Jawab:
L = ½ x (a1 + a2) x t
L = ½ x (4 cm + 10 cm) x 5 cm
L = ½ x 14 x 5
L = 35 cm.
Demikianlah pembahasan mengenai rumus trapesium, baik rumus luas trapesium dan rumus keliling trapesium lengkap beserta contoh soal dan bagaimana cara menghitung trapesium yang benar. Semoga bermanfaat dan bisa menambah wawasan pengetahuan kita semua tentang rumus rumus matematika.
Facebook Tweet Whatsapp